18일차 : 합성곱 신경망

합성곱 신경망¶

패션 MNIST 데이터 불러오기¶

In [1]:

from tensorflow import keras
from sklearn.model_selection import train_test_split

(train_input, train_target), (test_input, test_target) = \
    keras.datasets.fashion_mnist.load_data()

train_scaled = train_input.reshape(-1, 28, 28, 1) / 255.0 
# 채널차원이 있다고 생각한다.
# 흑백이지만 차원하나를 더 추가해 3차원으로 만들어준다.
train_scaled, val_scaled, train_target, val_target = train_test_split(
    train_scaled, train_target, test_size=0.2, random_state=42)

 

합성곱 신경망 만들기¶

In [2]:

model = keras.Sequential()

 

첫 번째 합성곱 층¶

In [3]:

model.add(keras.layers.Conv2D(32, kernel_size=3, activation='relu', 
                              padding='same', input_shape=(28,28,1)))
# 커널의 채널은 입력 데이터의 채널을 동일하게 따라간다.
# 배치 차원은 지정하지 않는다. (훈련할 때 마다 달라질 수 있으므로 같이 넣지 않음)

In [4]:

model.add(keras.layers.MaxPooling2D(2))

 

두 번째 합성곱 층 + 완전 연결 층¶

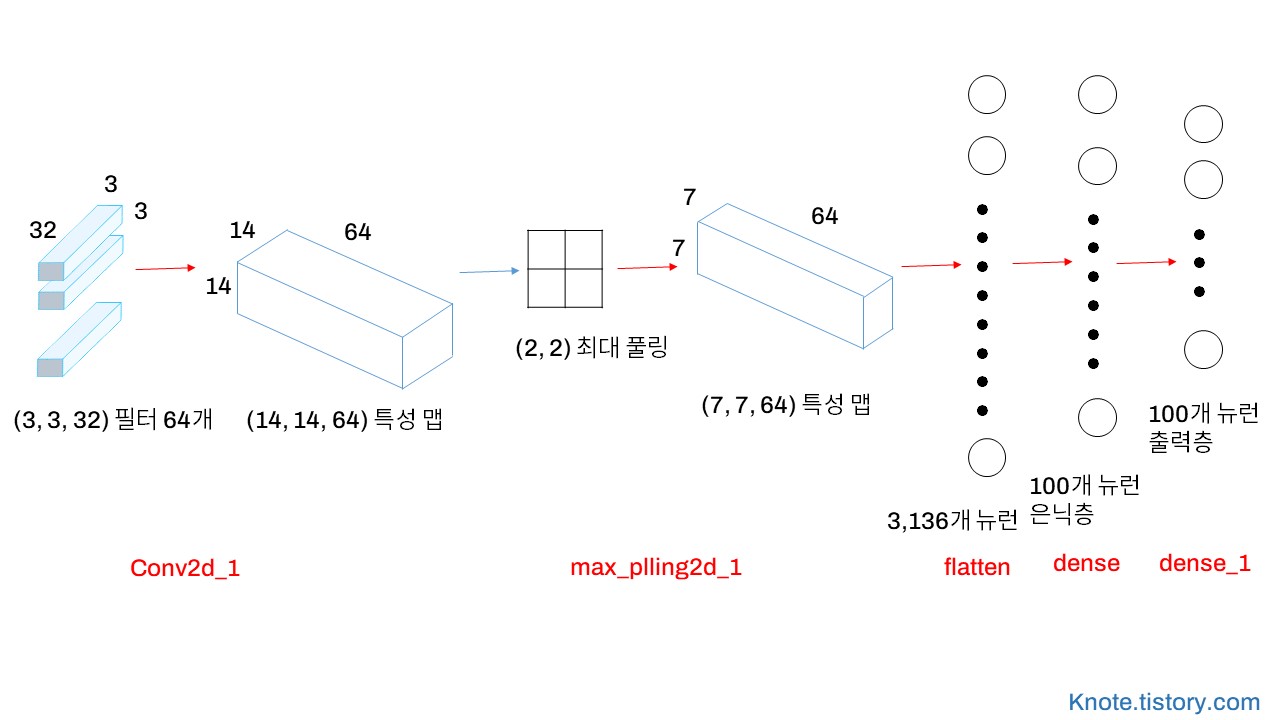
In [5]:

model.add(keras.layers.Conv2D(64, kernel_size=(3,3), activation='relu', 
                              padding='same'))
# 채널의 개수를 더 늘려 특성맵을 더 많이 만들어 다양한 특징을 많이 잡아내려는 의도
model.add(keras.layers.MaxPooling2D(2))

In [6]:

model.add(keras.layers.Flatten())
model.add(keras.layers.Dense(100, activation='relu'))
model.add(keras.layers.Dropout(0.4))
model.add(keras.layers.Dense(10, activation='softmax'))

In [7]:

model.summary()
# 완전연결층은 쉽게 과대적합 되기 쉽다
# 합성곱은 적은 개수의 파라미터로도 이미지의 특징을 잘 잡아낸다.

 

Model: "sequential"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 conv2d (Conv2D)             (None, 28, 28, 32)        320       
                                                                 
 max_pooling2d (MaxPooling2D  (None, 14, 14, 32)       0         
 )                                                               
                                                                 
 conv2d_1 (Conv2D)           (None, 14, 14, 64)        18496     
                                                                 
 max_pooling2d_1 (MaxPooling  (None, 7, 7, 64)         0         
 2D)                                                             
                                                                 
 flatten (Flatten)           (None, 3136)              0         
                                                                 
 dense (Dense)               (None, 100)               313700    
                                                                 
 dropout (Dropout)           (None, 100)               0         
                                                                 
 dense_1 (Dense)             (None, 10)                1010      
                                                                 
=================================================================
Total params: 333,526
Trainable params: 333,526
Non-trainable params: 0
_________________________________________________________________

 

합성곱 층 시각화¶

In [8]:

keras.utils.plot_model(model)

 

You must install pydot (`pip install pydot`) and install graphviz (see instructions at https://graphviz.gitlab.io/download/) for plot_model/model_to_dot to work.

In [9]:

keras.utils.plot_model(model, show_shapes=True, to_file='cnn-architecture.png', dpi=300)
# show_shapes=True사용하면 input과  output의 크기를 보여준다.

 

You must install pydot (`pip install pydot`) and install graphviz (see instructions at https://graphviz.gitlab.io/download/) for plot_model/model_to_dot to work.

 

모델 컴파일과 훈련¶

In [10]:

model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', 
              metrics='accuracy')

checkpoint_cb = keras.callbacks.ModelCheckpoint('best-cnn-model.h5', 
                                                save_best_only=True)
early_stopping_cb = keras.callbacks.EarlyStopping(patience=2,
                                                  restore_best_weights=True)

history = model.fit(train_scaled, train_target, epochs=20,
                    validation_data=(val_scaled, val_target),
                    callbacks=[checkpoint_cb, early_stopping_cb])

 

Epoch 1/20
1500/1500 [==============================] - 20s 13ms/step - loss: 0.5170 - accuracy: 0.8167 - val_loss: 0.3258 - val_accuracy: 0.8832
Epoch 2/20
1500/1500 [==============================] - 18s 12ms/step - loss: 0.3411 - accuracy: 0.8782 - val_loss: 0.2783 - val_accuracy: 0.8963
Epoch 3/20
1500/1500 [==============================] - 20s 13ms/step - loss: 0.2937 - accuracy: 0.8939 - val_loss: 0.2532 - val_accuracy: 0.9091
Epoch 4/20
1500/1500 [==============================] - 18s 12ms/step - loss: 0.2615 - accuracy: 0.9054 - val_loss: 0.2422 - val_accuracy: 0.9113
Epoch 5/20
1500/1500 [==============================] - 19s 12ms/step - loss: 0.2394 - accuracy: 0.9123 - val_loss: 0.2253 - val_accuracy: 0.9181
Epoch 6/20
1500/1500 [==============================] - 18s 12ms/step - loss: 0.2163 - accuracy: 0.9211 - val_loss: 0.2286 - val_accuracy: 0.9185
Epoch 7/20
1500/1500 [==============================] - 19s 13ms/step - loss: 0.2012 - accuracy: 0.9260 - val_loss: 0.2222 - val_accuracy: 0.9178
Epoch 8/20
1500/1500 [==============================] - 20s 13ms/step - loss: 0.1854 - accuracy: 0.9311 - val_loss: 0.2192 - val_accuracy: 0.9198
Epoch 9/20
1500/1500 [==============================] - 19s 13ms/step - loss: 0.1718 - accuracy: 0.9369 - val_loss: 0.2273 - val_accuracy: 0.9222
Epoch 10/20
1500/1500 [==============================] - 20s 13ms/step - loss: 0.1585 - accuracy: 0.9402 - val_loss: 0.2330 - val_accuracy: 0.9204

In [11]:

import matplotlib.pyplot as plt

In [12]:

plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.xlabel('epoch')
plt.ylabel('loss')
plt.legend(['train', 'val'])
plt.show()

 

 

평가와 예측¶

In [13]:

model.evaluate(val_scaled, val_target)
# [손실, 예측]

 

375/375 [==============================] - 2s 4ms/step - loss: 0.2192 - accuracy: 0.9198

Out[13]:

[0.21923945844173431, 0.9198333621025085]

In [14]:

plt.imshow(val_scaled[0].reshape(28, 28), cmap='gray_r')
plt.show()

 

In [15]:

preds = model.predict(val_scaled[0:1]) 
# 마지막 덴스 층 (예측한 확률)
# 입력되는 값은 첫번째 배치차원이 있다고 생각한다. 슬라이싱 연산자를 쓰는 이유 1*28*28*1
print(preds)
# 9번 째 요소 가방 확인

 

[[4.0173234e-18 1.3420832e-24 2.1657030e-19 3.5420750e-16 9.2692958e-15
  5.0576039e-20 3.5442224e-17 1.5183595e-20 1.0000000e+00 7.7842200e-20]]

In [16]:

plt.bar(range(1, 11), preds[0])
plt.xlabel('class')
plt.ylabel('prob.')
plt.show()

 

In [17]:

classes = ['티셔츠', '바지', '스웨터', '드레스', '코트',
           '샌달', '셔츠', '스니커즈', '가방', '앵클 부츠']

In [18]:

import numpy as np
print(classes[np.argmax(preds)])

 

가방

 

테스트 세트 점수¶

In [19]:

test_scaled = test_input.reshape(-1, 28, 28, 1) / 255.0

In [20]:

model.evaluate(test_scaled, test_target)
# 합성곱층, 풀링층, 드롭아웃층을 잘 찾아야한다.

 

313/313 [==============================] - 2s 5ms/step - loss: 0.2346 - accuracy: 0.9189

Out[20]:

[0.23460885882377625, 0.9189000129699707]

출처 : 박해선, 『혼자공부하는머신러닝+딥러닝』, 한빛미디어(2021), p422-441